白熊泡面🍜

Chain of Intelligence如何得到智慧？

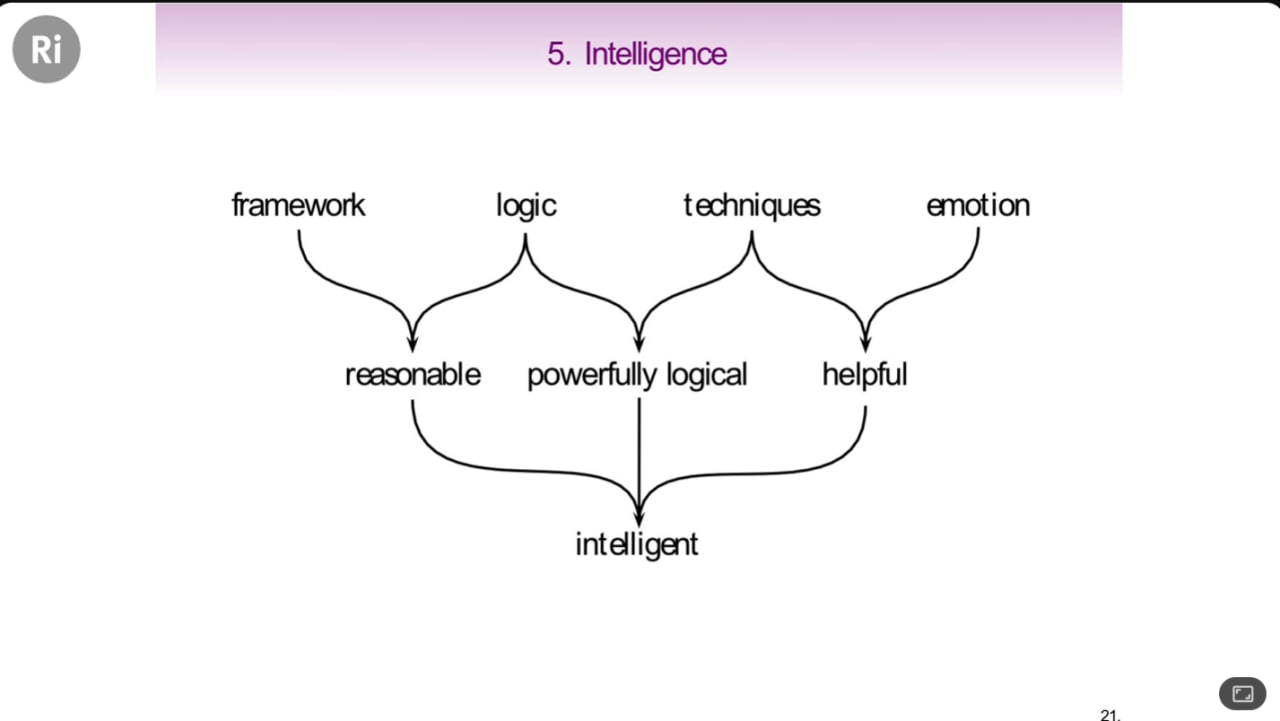
Eugenia Cheng 尝试用范畴论提炼出与智慧有关联的东西，她认为是要合乎逻辑+有强大的推理能力+乐于助人。
Eugenia告诉我们，逻辑是从一些假设的概念出发，然后你来推论这些假设是否成立。[有人说你在假设一些没发生的事，那就意味着你不符合逻辑。]Eugenia表示这不是True.[有些人说他们不相信同性恋婚姻，因为他们认为婚姻是男人和女人之间的事情。]听起来很有逻辑，但只是把同样的一个事情讲了两次。因为他们不相信同性恋婚姻，所以认为婚姻不是同性恋的事情。类似的逻辑还有[我喜欢这张桌子，因为我喜欢这张桌子。]
以上逻辑都是逻辑，但不是假设能够成立的那种合乎逻辑，合乎逻辑Reasonable是要求你使用逻辑Logic，而且有一个Framework框架用来测试自己假设的逻辑是不是合乎逻辑。

而强大的推理能力，指的是推理的链路很长，[我喜欢这张桌子，因为我喜欢这张桌子。]这种推理就只是在原地踏步。但如果你能从一个非常漫长的角度来解释事情到底为什么会发生，把某个事件某个案件追溯到First Principle，你就破案了！(智慧女神在向你招手)
因此Powerfully Logical 是需要你使用逻辑，并且有技术地让思维走得很远，把每一个孤立的点串成线。

至于乐于助人（宜人性），Eugenia Cheng解释到如果你只是坐在那里完成一个又一个对任何人都没有帮助的逻辑推论，这意味着这个人是不太聪明的样子。
聪明机智需要的乐于助人要求你投入情感，同时提供帮助人的技巧，这又需要你识别出他人的困难和需求。你要看见他人的难处，而不是施舍自己拥有的但别人不需要的。Eugenia Cheng举例我们的教育制度，老师如果不投入情感，就只会教授一些冷酷的知识点，要求学生遵守这些那些规则，导致学生在学一些东西的时候就会没有感觉，听不进去。是什么导致老师无法乐于助人呢？有可能是老师本身很古板，也可能是老师也需要遵守一些古板的规定，老师必须要满足某些课程标准才能不扣奖金拿到工资。老师必须给学生出测试题、确保学生能通过测试，于是在规定下，学习变成了没完没了的试卷和小测小考期中考期末考全市统考全国高考。这一切会让大部分老师和学生在一场徒劳的战斗中，陷入情绪低落的状态。因为它遵守了规则，却违背了人的情感体验。而情感是出于真实的，前面提到的逻辑则是从假设出发的。(你面前有一个屎味巧克力和巧克力味的一坨便便💩，情感上大部分人会感到恶心两个都不想吃，但如果老师不投入情感也觉得它恶心，老师就只会视而不见逼学生吃光它们，一点也不许剩。)

Chain of Stupidity 如何实现愚蠢？

Eugenia Cheng表示还存在一个愚蠢理论：每个群体都拥有相同比例的蠢货，不管是街道小贩、清洁工、警察还是领导、政客，蠢货的比例都是一样的。

把愚蠢和聪明的程度定义在坐标系上，x轴是利己，y轴是利他。如果你只选择利己而损害了他人，那么你是强盗，50%的愚蠢；如果你只选择利他而伤害了自己，大家会说你很不幸，留下了自己的老婆孩子就这么牺牲了，那么你是烈士，50%的愚蠢;Eugenia Cheng想了很久，因为她觉得为别人牺牲是高尚的行为啊，多数女人和某种拥有高尚精神的男士都会这样做，他们都把别人放在了第一位😢。
但如果你不利己也不利他，那就是100%的愚蠢。而最后一个象限，如果你利己又利他，就是这个愚蠢理论的反面例子，一种有机制聪明的选择。

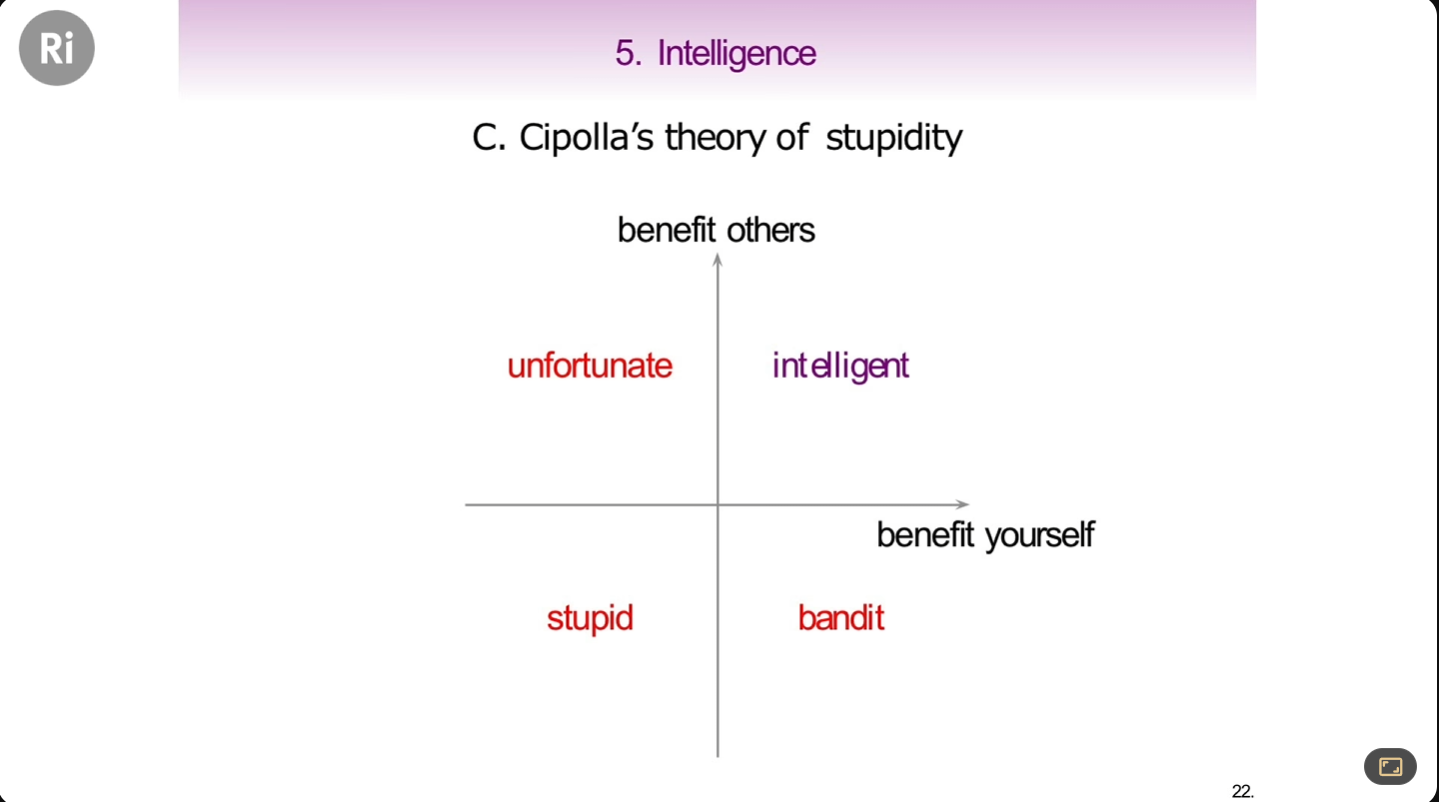
Eugenia Cheng认为当你的感受和行为共同作用，尽可能做一些利己又利他的行为，就会形成良性循环，帮助自己远离愚蠢。

🐉来源：英国皇家科学院讲座How to Think Like a Mathematician

#【Eugenia Cheng的范畴论】
如果我们不将性别与个性分开，我们就无法进行控制实验，因为我们会混淆问题。这种缺乏明确方向的问题，会迫使我们进行一种元讨论。

比如说，一些人认为所有人类女性共同拥有的属性只能由那些拥有特权的女性定义：白人女性（或者更确切地说，富裕的白人女性，不管异性恋者或是同性恋者）。

但是一些人又说，世界上还有许多其他问题，比这些女性问题更严重，比如种族主义，恐同和经济不平等诸如此类的。于是我们被哪个问题更重要这样紧张激烈的辩论分散了注意力。

我怀疑，唯一从这些元讨论中受益的是那些掌握权力并且想要保持权力的人。女性们在女权主义的含义上争吵，争论谁给予了哪个女性团体更多空间，以及争论谁遭受了最严重的虐待和伤害。

除此之外，被歧视的人们 - 根据种族、性取向、财富和社会地位、教育、学识、性别、体能和运动能力进行分类，都努力发出自己的声音。任何感到不公的人们都表达他们的不同意见，而权威们则高兴地摩拳擦掌，巩固着他们的权力。

幸运的是，数学在定义和处理元讨论时非常有用。在数学中，我们提出一种理论，提供一个基本定义，通过探索一些关键例子进行说明。然后通过证明该理论的无处不在和实用性来证明它的有效性。

这是有用的，因为它能够解决特定的问题，能够更清晰思考。我在这里提出的范畴论同时做到了这两点。

例如，方程式1 + 2 = 2 + 1类似于方程式2 + 5 = 5 + 2。但在数学中，我们说：对于任何数字a和b，都有a + b = b + a。这种抽象一方面有助于澄清概念，另一方面也开放了一种概括，涵盖了更多未知的例子。

也许我们尚未发现是什么导致了某个女性不爱发言的行为，也不知道如何进行干预以进行改变她。但是通过识别重复出现的原因，去除不相关的细节，并集中力量在重要的问题上，我们就已经迈出了第一步。这是构建一个良好理论的基本前提。抽象也可以帮助我们思考模式背后的原因。

数学是不断思考为什么，不断深入挖掘，寻找更加基本答案的过程。对于为什么女性在混合团体中倾向于说话较少，一个肤浅的答案可能是：“因为她们是女性”。如果我们将这个理论置于实践中，很可能会发现有些女性其实能够表达自己的声音，而有些男性反而不能表达自己。

或许我们会发现在性别和发言能力之间存在统计相关性，但在抽象的数学中，我们试图深入探究：为什么作为一个女性在统计上会导致这种现象？如果这仅仅是一个统计相关性，而不是真正的因果关系，我们是否能够进一步挖掘并找到因果关系？按照这种方法进行，【我们会发现，是或不是女性并不是那么重要，关键是人与人之间的关系，以及不同个体之间如何相互作用。】（有人喜欢在陌生的场合发言吹牛，有人只喜欢在有熟人的场合聊天发言）

【把重点放在关系而不是内在特征上的思想】，在现代数学中与一个重要的进展相等：范畴论的兴起，也是我的研究领域。【范畴论】的思想被认为是数学的一个“基础”分支，因为它研究数学的运作方式。在这之前有集合论，它有着不同的意识形态和非常不同的技术方面。【集合论】基于数学起源于成员关系的思想，即一切都始于询问一个特定元素它是否属于一个特定集合。

你可以把它想象成某些人不顾一切想加入组织的困扰（火速结婚生子拥有一个家），无论是字面意义上的俱乐部，比如那种老式而独特的绅士俱乐部，还是更抽象的政治"部落"，这是那些拥有相同观点的人共享归属感而建立的。

范畴论则有一个不同的出发点：关系。它基于这样一个观点，通过观察事物或人与周围环境的关系，我们可以理解它们的很多方面。一个集合可以被表示为一个闭合线中的元素集合，其内在特征决定了包含和排除关系。有点像一个家谱，只是我们不是看父母和子女，而是看哪些数字与其他数字之间有关系，如因子。

从某种角度来看，这只是一个微小的观点转变，然而它给现代数学赋予了新的方向。回到我们的话题上来，集合论的一种方法是基于一些内在特征来定义地球上的女性群体，这些特征可以是染色体、生殖器官或激素，具体取决于说话者的关注点。实际上，除了它们并不完全等价之外，这些定义都不像人们想象的那样清晰明了。因此，我将采用范畴论的方法，即关注人们如何相互作用而不是他们的生物描述。

🐉来源：《X+Y. A Mathematician’s Manifesto for Rethinking Gender》 - Eugenia Cheng #书摘 #读书會

如何在世界中找到意义和下决定？

生活非常复杂，有许多不可预知的事件，结果就是我们经常陷入逻辑，无法自拔，即容易犹豫不决，难以下决定。

为了做决定，我们可以采取几种方法：

1/因为逻辑太慢而时间有限，可以尝试向系统添加更多公理或者偏好，以便快速将选择限制为一个。比如最便宜的选择？没有尝试过的选择？或者就丢一枚硬币决定，或者选择脑袋里根本挥之不去的那个选项！

2/内化你的逻辑，将逻辑转化为直觉，用直觉来决定。

紧急情况下，我们必须迅速决策，如果有火灾，我希望你能直觉反应出“我必须逃出去！”这是瞬间的本能反应，它可能并非完全经过逻辑处理。但它也不是不合逻辑。即使你不用每次都经历逻辑步骤来得出这个结论，因为你已经内化了它们。

另一方面，我认为我们都可以达成共识，这有一个不合乎逻辑的推论：[有
一场火灾发生在这里，我会待在这里。]，这是决定不会选择的决策。

通过感觉来获取信息通常比通过逻辑获取信息更快，这就是为什么我认为
成为一个强大的逻辑思考者的一种方法是将逻辑转化为感觉，就像在城市
中凭借感觉或直觉找到路一样，不一定需要能做到绘制整张地图。

在紧急情况下，也可能没有足够的时间进行必要的逻辑推理或收集必要的信息。例如，有人断言，提高所得税不会带来更多收入，因为最富有的人会选择离开这个国家。这可能是正确的，但我们无法确定人们会真正做什么，这只是猜测，而非内化的逻辑。

当天气预报出错时，我们不应过分责怪气象预报员，因为实际上，天气预报系统超出了逻辑的掌控范围。原则上我们可能完全理性理解世界，但实际上这种情况永远不会发生，因为我们几乎肯定永远不会拥有足够的信息。

一个以前看起来可信的人也可能在后来失信。有时候你只能凭直觉决定是否相信某人。

3/超出逻辑合理范围的情况，要使用其他方法->Axiomatising公理化，而不是假装非逻辑的事物是逻辑的，但也不应该判断那些非逻辑的事物是坏的。

数学领域最著名的公理是欧几里德的五条最基本的几何公理，这可以推导出几何所有规则。

而个人的公理是核心信念，我们可以先思考[我们相信什么事物是真实的？]->尝试将真实的事物归纳为基本信念->从中推导出一切的概括。任何观点都是可行的，只要它不引起逻辑矛盾，否则你的信仰会就此崩塌。反复询问“为什么？”的过程是揭示某事物背后深层逻辑的方法之一。

这也是理解数学的一种方式：如果我们问物理世界的某些方面为什么会按照它们的方式运作，这些问题可能会被科学解答。
如果我们询问人类世界的某些方面为什么会以这种方式运作，我们可能最终会进入心理学，甚至哲学领域。
要回答关于信仰的“为什么？”这类问题需要我们具备一定的逻辑能力，以便
我们能够揭示逻辑推论的长链，同时还需要有自我意识。另一方面，要了解他人的公理是什么，我们需要具备逻辑能力和同理心。

我的个人公理可以分为三个主要领域：
1.仁慈：我相信善待他人。基于此，我得出了其他关于帮助他人、为社会做贡献、教育、平等和公平的信念。
2.知识：我相信我们能建立起来以获取各种不同学科知识的框架。所以我相信科学研究和历史研究。

3.存在：我相信我们存在，主要是为了继续生活。对于这一点，我不太确定，而且我怀疑如果我相信相反的观点（我不存在）也不会有太大区别，所以我选择把它放进来，因为它似乎比相反的观点对我更有帮助。至少对我很重要，因为这意味着如果我认为证据合理，那么我可以信任依靠一些事物。

总体而言，这并不完全合乎逻辑，因为我没有将所有这些结论追溯到它们
的逻辑起源。例如，我相信引力，尽管我并不在源头上理解它。正如我们将看到的，这可以帮助我们确定更复杂的信念，并明确为什么其他人可能与我们在某些更复杂的信念上意见不合。

- 【类比的工作原理】

在数学中，通过明确表达抽象可以获得巨大的力量，这意味着我们可以进行更复杂或微妙的类比。

一个现实中很真实的例子：[底层人民的人生经历是否类似？]，它的答案是模糊又微妙的：这取决于你用多高维的抽象层级来思考这个问题。每个人都将选择适合自己观点的抽象阶层，并拒绝思考其他阶层的有效例子，于是就常常出现分裂的争论。

类比可以帮助我们理解个人信念是什么，他人的信念又是什么。

当我们讨论性骚扰问题时，一些人担心如果所有指控都被认真对待，那么会导致一些人（男性比较多）遭受污名指控，即使他是无辜的。然而，现实又存在一个严重问题，即一些人（男性比较多）仍然逍遥法外，给另一些性侵受害者（女性比较多）带来了不必要的痛苦。

没有人应该经历被冤枉或被性侵这种痛苦和创伤。我相信我们应该更加关注这些没有被制止的犯罪行为上，而不是混淆视听去争论【被污名指控】和【被性侵】哪个更糟糕一点。

我们可能认为我做某某事，基于个人准则，而非偏见。如果这是真的，那么我们可以转移到类似情况，应用这个相同的个人准则，如果情况不成立，说明我不是在遵守个人原则，而是遵守了个人偏见。

下面用一个科学与宗教的争论来做类比测试。

许多科学家蔑视宗教，依据是宗教人士在没有科学证据支撑下相信了某些东西，他们相信只是因为某本书这么写了或者宗教领袖告诉他们的。

然鹅，权威的科学家也是如此要求我们以类似方式相信某些东西，科学发现可能有某些支撑性证据，但不对科学家以外的群体公布所有的研究数据，让我们得以亲自验证所有研究。只是要求我们相信他们，相信书籍和期刊上写的内容数据，就像宗教领袖要求人民相信他们传教的内容，相信圣经写的内容一样。

情况开始变得微妙，我们似乎找到一种更加有效的方式来了解[为什么那么多人相信宗教]，尽管一些权威科学家会说[信宗教的人都是蠢货]。

如果科学家要论证科学比宗教更可靠，他们需要找到一个更细致的中间原则来区分它，这样宗教和科学就不是类似的了。这个中间原则也许是：除非这个实验或现象/证据可以复制复刻，否则我们不应该仅仅相信老师或书本。

回归到最前面的话题，如何关注没有被制止的犯罪行为？逍遥法外的犯罪者会用他的一生不断复制他的罪行，而他身边会存在类似的受害者，类似的痛苦。

🐉来源：《The Art of Logic》 Eugenia Cheng #RI #math